Originally published: 30 September 2006
Last modified: 7 March 2018
I rant about people defending Pluto’s planethood elsewhere on this site, but I’d like to address one of the flaws of the new definiton…
In “Definition of a Planet in the Solar System” (Resolution 5 of the XXVIth General Assembly), the International Astronomical Union (IAU) resolved that: “A planet is a celestial body that (a) is in orbit around the Sun, (b) has sufficient mass for its self-gravity to overcome rigid body forces so that it assumes a hydrostatic equilibrium (nearly round) shape, and (c) has cleared the neighbourhood around its orbit.”
Obviuosly, the weak part of this definition is (c), with the highly unsatisfying phrase, “cleared the neighbourhood around its orbit.” I don’t see this as a fatal flaw, however, and there’s already a reasonable proposal to fix it. In what follows, I’m basically just re-iterating arguments presented by Steve Soter, whose “What Is a Planet?” article describes things in much greater detail.
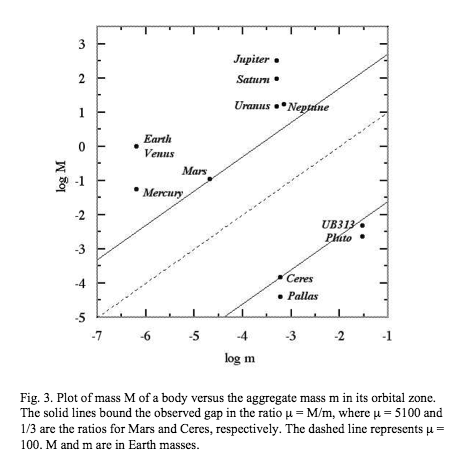
In the simplest argument, Soter defines a quantity μ to be the ratio of the mass of the object to the aggregate mass of all the other bodies that share its orbital zone. (For you sticklers out there, “two bodies share an orbital zone if their orbits cross a common radial distance from the primary, and their non-resonant periods differ by less than an order of magnitude.”) What’s nice about μ is that solar system objects neatly divide into “planets” (with values of mu between 5,000 and 2,000,000) and “dwarf planets” (with values less than one). I reproduce his Figure 3 below:

Note the neat dividing line between “planets” and “dwarf planets.” (And this is in logarithmic space, so the differences are huge!)
A more complicated argument relies on a quantity Λ defined by Stern and Levison 2002 (“Regarding the criteria for planethood and proposed planetary classification schemes” in IAU Highlights of Astronomy 12, pp. 205-213):
Λ = kM2/P
Where M represents the scattering object’s mass and P its orbital period; k is “approximately constant.” Basically, Λ represents the time it will take for stuff to scatter out of an object’s orbit compared to the age of the Universe (to complicate things a bit, Λ is proportional to the latter quantity and inversely proportional to the former). Basically, an object with Λ > 1 will have scattered most stuff out of its orbit. Now check out Figure 1 from Soter’s paper:
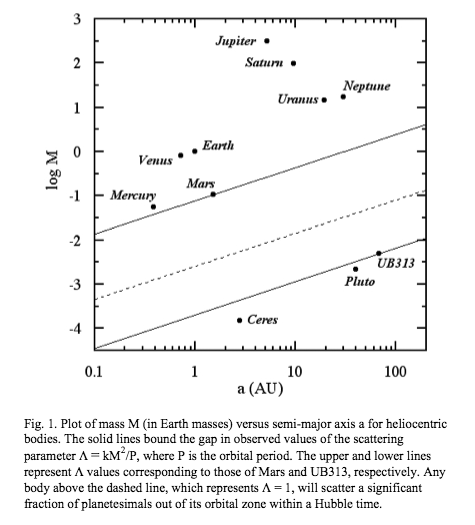
The separation between the “planets” and “dwarf planets” remains significant and easy to distinguish. (And again, this is in logarithmic space.)
If nothing else, Soter’s paper shows that one can define planet rigorously and quantitatively, and thus, it seems reasonable to believe that at IAU definition can be fixed. Critics claim that this is a dynamicist’s approach, but since “planets” started out as “wanderers” in the night sky, doesn’t a dynamical definition make sense?
Email Ryan if you have any questions, comments, concerns, or gripes about this page.